本章将讲述混沌是怎样产生的,以及混沌的几何图景。由于有很多新概念,本文将注定冗长而晦涩。
二维相图的解析
还记得我们在上一章所得出的摆的相图吧?那个在平面图上看起来像眼睛,随后我们又让它分别处在圆筒和U形管上的东西。这东西看起来很奇怪,那就使用更简单的例子来描述非线性运动,假设我们只针对两个自由度的问题进行分析,得到如图1所示的相图。不过相对于无摩擦摆的相图,该系统是有摩擦的,即非哈密顿系统。
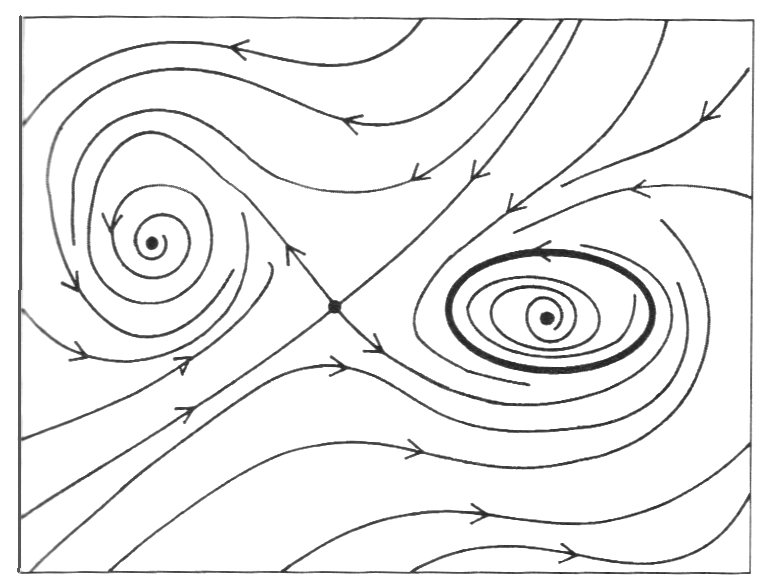
图1 平面内流的相图
之所以将图1称为流的相图,已在上一章说过,多数非线性动力学中的运动都可以虚拟为流体的流动,从不同的初始条件出发,就相当于从流场中不同的位置出发,可以得到不同的轨线,此轨线也相当于流场中的流线。图1这样的相图描述了微分方程解的情况。如果选定从一个初始点出发,顺着流线到了下一个点,则第二个点就是在以初始点为初始条件时微分方程的解。例如,在用计算机进行数值计算时,可以根据以一个用常微分方程描述的速度场,利用欧拉法或隆格-库塔法追踪此流线,即相当于求解此常微分方程。图1展示了许多流线,即在不同的初始条件下微分方程解的情况,该图同时反映了这些流线相互配合的情况,因此称作方程的相图。在此图中,相邻曲线的形状和方向相近,这说明运动是连续的,没有任何一个概念流体粒子被撕开朝不同的方向运动。
在该图,还有如下 4 个特征:
- 图的左边有一个点,所有邻近流线以螺旋形向它靠拢,该点称作汇。
- 右边有一个出水孔,所有邻近流线以螺旋形离开,该点称作源。
- 中间有一个似乎是流线发生交叉的点,该点称作鞍。
- 右边的源被一个闭合的环围绕,流体沿着该环转圈,这是极限环。
典型地,平面流只有这 4 个基本特征。这也是具有 2 个自由度的微分方程所拥有的特征。
图2 汇 图3 源 图4 鞍 图5 稳定极限环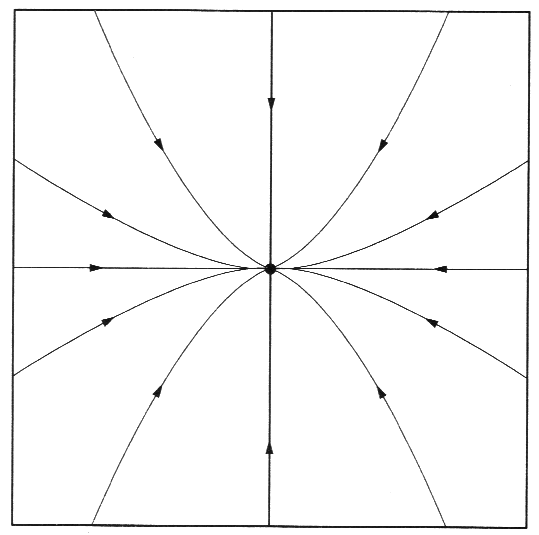
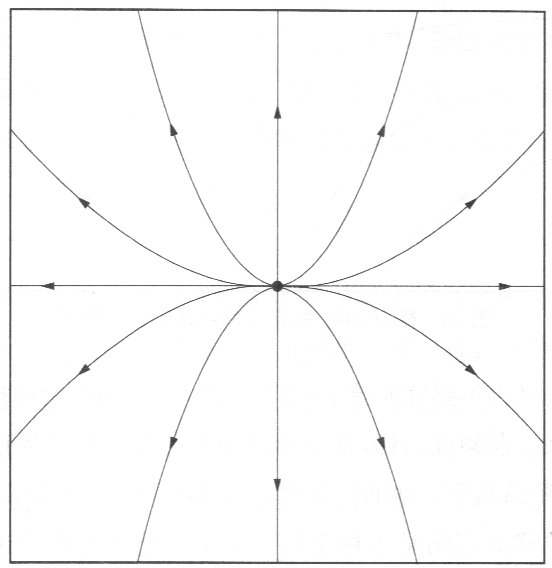

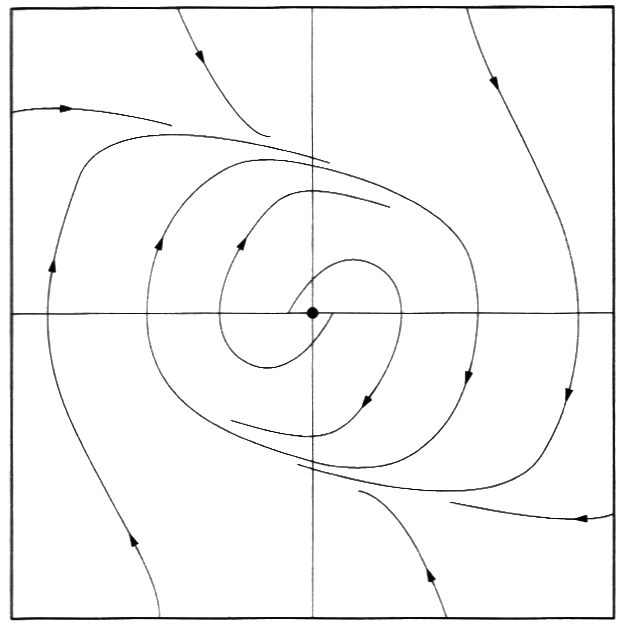
图2至图5是这 4 个特征的图示。让我方先来认识这 4 个基本特征吧:
- 汇。流线在汇处退化为单个点,所有邻近的流线都指向它。汇本身代表系统的定态,并且是稳定的定态(小扰动作用下流体粒子可能偏离汇,但最终会回到汇)。
- 源。流线在源处退化为单个点,所有邻近的流线都离它而去。源也代表系统的定态,但是是不稳定的定态。
- 鞍。鞍就像山脉中类似于马鞍的隘口。流线在鞍处退化为单个点,有些邻近的流线指向它,又有些离它而去。鞍也代表系统的定态,但在有些方向是稳定的定态,另一些方向则是不稳定的定态。通过鞍点的流线称作鞍的分界线。如果沿着鞍的分界线趋近鞍点,流体粒子并没有被撕开,但接近鞍点时流速变得无限缓慢,需要无限长的时间才能到达,所以在鞍点处流线并未交叉。
- 极限环。在极限环上,运动是周期性的(因此它不是系统的定态)。有两类极限环:稳定极限环,邻近点都向着它移动(图5);不稳定极限环,邻近点都离它而去(将图5中所有箭头反向就是不稳定极限环)。
以上的归纳是庞加莱作出的。庞加莱还和一位叫本迪拉克的瑞典数学家共同证明了一条定理:
在平面内的微分方程组中只典型地存在 4 种类型的性态。
所谓“典型地”,指的是微分方程并非只有这 4 种特征,还有其他例外的特征。但这种例外就像抛一枚硬币,碰巧在硬币落下时立在边缘上一样少见。
此外,还有一种运动值得一提,就是拟周期运动。如月亮绕着地球转,地球绕着太阳转,则月亮相对于太阳的运动就是这两种周期运动的合成运动。仅当两周期之比是有理数时,合成运动具有周期性;否则,将不具有周期性,但极其接近于周期运动,因此称这种运动为拟周期运动。
拟周期运动在一般动力学系统里不是定性的,但却常出现在经典动力学中。从拓扑学上来看,拟周期运动发生在环面上,就像炸面圈,如图6。
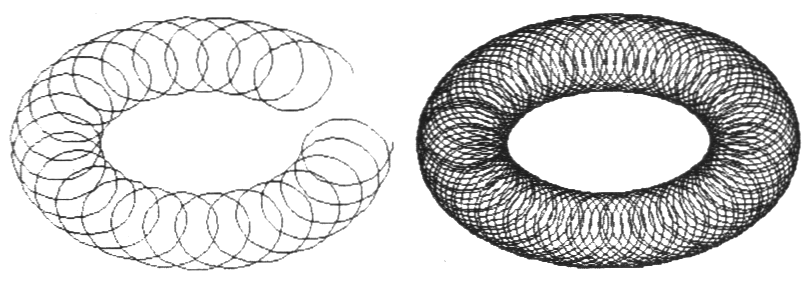
图6 拟周期运动
高维空间
吸引子
现在,我们很自然地设定新目标:考察在三维以三维以上空间中微分方程系统的形态,或系统相图的特征。
仅就三维空间而言,情况已经更复杂了。比如,三维空间中存在的纽结就是平面内所没有的。庞加莱在这方面的研究开了个头。他发现三维空间内所有可能的典型的定态类型:源、汇和两种不同类型的鞍。鞍或者有一个外向运动点的面和一条内向运动点的线,或者有一条外向运动点的线和一个内向运动点的面。另外,其实三维空间中的极限环也有三种:稳定极限环、不稳定极限环和鞍状极限环。
看起来就这些,没有人发现过任何其他典型的流特征。
斯梅尔对高维空间微分方程系统的形态做了深入的研究,并提出了许多新观点。为了强调新观点,斯梅尔用术语“动力学系统”代替“微分方程系统”。他研究动力学系统时所根据的是他们的几何特征——相图的拓扑特性——而不是根据定义他们的公式。斯梅尔做的第一件事,是给“典型的”界定一个精确的内涵。他创造了“结构稳定性”术语来形容动力学系统发生微小的变化时,其拓扑特性不发生改变的性质。
现在我们讨论稳定性,可能指的是两个不同的内容。第一个是给定方程的定态的稳定性,方程的定态是方程的一个解,其稳定性指的是在初始条件发生小变化时是否仍能回到此定态。第二个结构稳定性,它是整个系统的属性。
三维空间的源、汇、2种鞍、3种极限环都是结构稳定的动力学系统。而其他拓扑结构,往往是不稳定的,如图7所示,具有3条分界线的鞍在小扰动下解体,形成3个分开的鞍和一个汇。
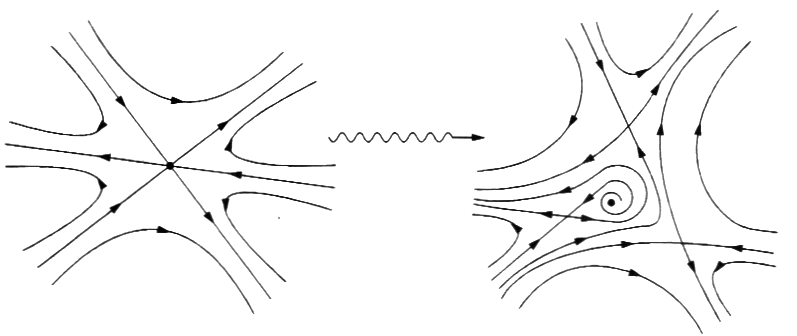
图7 结构稳定性
在斯梅尔看来,动力学系统最重要的属性是它的长期性态。而非长期性态可称为“暂态”,有时候,暂态也很重要,如当拟打开计算机开关时,由于浪涌导致的错误暂态可能会毁掉一块电路板。
那么,系统的长期形态会是什么样的呢?答案是:它稳定下来成为吸引子。吸引子是……它稳定下来成为的任何东西。吸引子的实质在于,它是相空间的某部分,从它附近出发的任何点都逐渐趋近于它。另外,吸引子不能解体成为两个都满足这一定义的较小子集。如不能把汇和极限环组合后视为单个吸引子。
就平面内的结构稳定系统,其中的源、汇、鞍和极限环都是吸引子。或者说,吸引子要么是点,要么是稳定极限环。再或者说,吸引子要么是静止的定态,要么是周期性地重复某种运动系列。
那么,在高维空间,是否真的也只有点和极限环才是吸引子?
庞加莱截面
在高维空间中思考轨线的形态实在是太困难了,我们必须找到一种有效的思维模式——借助庞加莱截面进行降维。我们在第 4 章中已提到过庞加莱截面,这里再继续深入,看看庞加莱截面的本质是什么。
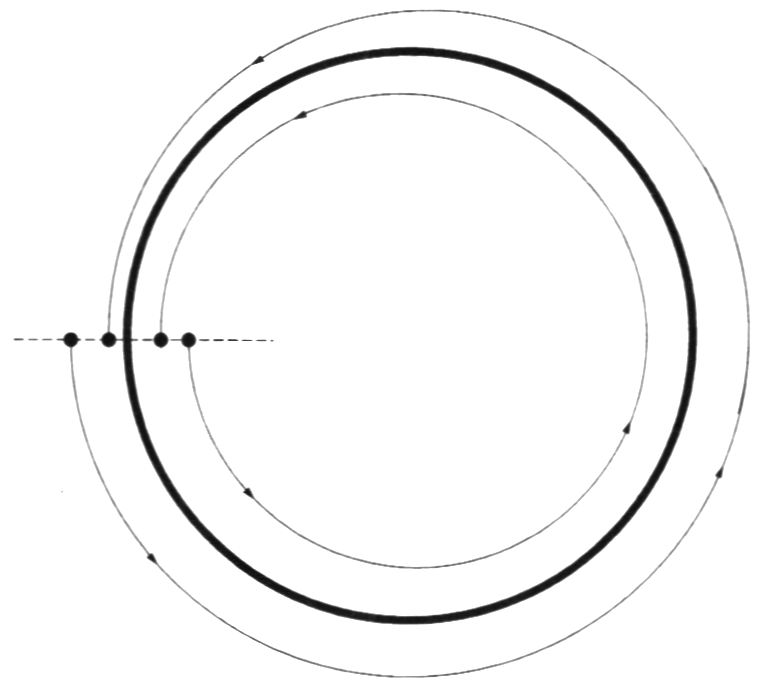
图8 通过极限环的庞加莱面
考察平面内一个具有稳定极限环的系统,该极限环就是一个周期吸引子。画一条切割极限环的短线段,则线段上任意点从该线段出发,循环一周再次回到该线段时,必然更加靠近极限环,或者直接到达极限环处(图8)。虽然称作线段,但该线段就是庞加莱截面。这种从线段上一点出发,经过连续变化,再次返回线段的过程,实际上相当于从线段到自身的连续映射。当存在穿过线段的极限环时,这种映射使线段缩向线段与极限环的交点。
现在把问题改一下,假设我们只有一个线段,并不知道是否有穿过此线段的极限环。我们还发现,从该线段出发的点,沿着轨线运动会,总是能再次返回该线段,即系统的运动可解释为是线段到自身的连续映射。那么,是否存在一个穿过线段的极限环呢?答案是存在。因为拓扑学中有一条定理:每一线段向自身的连续映射,必至少有一个不动点,即映射到自身的点。该定理的原理类似于中值定理,其深层机理是“流体”是连续扯不开的。因此,如果存在一条线段,从它上面出发的每一点最终都回归,则至少存在一个通过此线段的周期解。
再来看看三维空间。三维空间中的庞加莱截面不再是一个线段,而是一个曲面。典型地,这是一个拓扑盘——一个没有洞的小曲面。从盘向自身的映射极其复杂,但却和线段映射一样,它也必然存在不动点。或者说,具有盘样庞加莱截面的三维流,必有穿过盘的周期轨线。
更一般地,对于 n 维空间,庞加莱截面是一个 n- 1 维的超盘。数学家劳威尔曾得出一个相当艰涩的不动点定理,从中可得出结论:至少有一条周期轨线穿过该超盘。
到目前为止,我们仍然没有找到除了点和极限环之外的吸引子。
奇怪吸引子
让我们继续搜寻其他类型的吸引子。以上基于庞加莱截面寻找极限环的过程中,映射过程似乎都没有使庞加莱截面发生大的扭曲变形。为了能找到其他类型的吸引子,我们必须使用不同类型的映射。
包绕映射
考虑如下一个简单的动力学系统:
“假设有一个在圆上运动的点,圆的周长正好是 1,选定一个固定的零位置,点在圆上的位置就是该点和零位置之间的圆弧长度,用 x 表示,则 x 总是介于 [0, 1] 之间的一个数。现在规定点服从下述动力学定律:如果在给定的时刻它在位置 x 处,则在下一时刻它运动到 10x 处。试分析点的运动特征。”
说明一下:在该运动中,点在每一时刻的位置是对其自身的迭代。注意每次得到的 x 值并不是 $x_0$, $x_1 = 10x_0$, $x_2 = 10x_1$, $x_3 = 10x_2$, ……。这是因为 x 总是处于区间 [0, 1] 之间,用该公式所得的 x 将很快超过此区间。每个时刻所得到的新位置总应该从原来的零位置算起。
那么,该如何用几何方法寻找每个时刻点的位置呢?答案是可以构建这样一个螺线管模型来寻找:
- 假设我们原始的周长为 1 的圆周是一个可以随意拉长(你或者想象在拉长过程中它变细了)的封闭圆圈。圆圈上标记两个位置,一个实零点位置,另一个是当前时刻点所处的位置。
- 让我们把该圆圈拉长为原来的 10 倍,并将其折叠 10 次形成一个圆,该圆的圆周有 10 条细线,周长仍为 1,并将该圆缠绕在原来的圆上(相当于包绕自身 10 圈),形成一个螺线管,使其零点仍与原来的零点对应。如图9所示。
- 在拉长、折叠和缠绕后,所考察点的位置变化了,此时考察点相对于原始零点的圆弧长度就是其新的位置 x。
- 在下一时刻考察点的位置时,再次将已经拉伸且封闭的圆圈拉伸 10 倍,折叠 10次,缠绕在螺线管(相当于包绕螺线管 100 圈),考察点的位置。如此反复迭代。
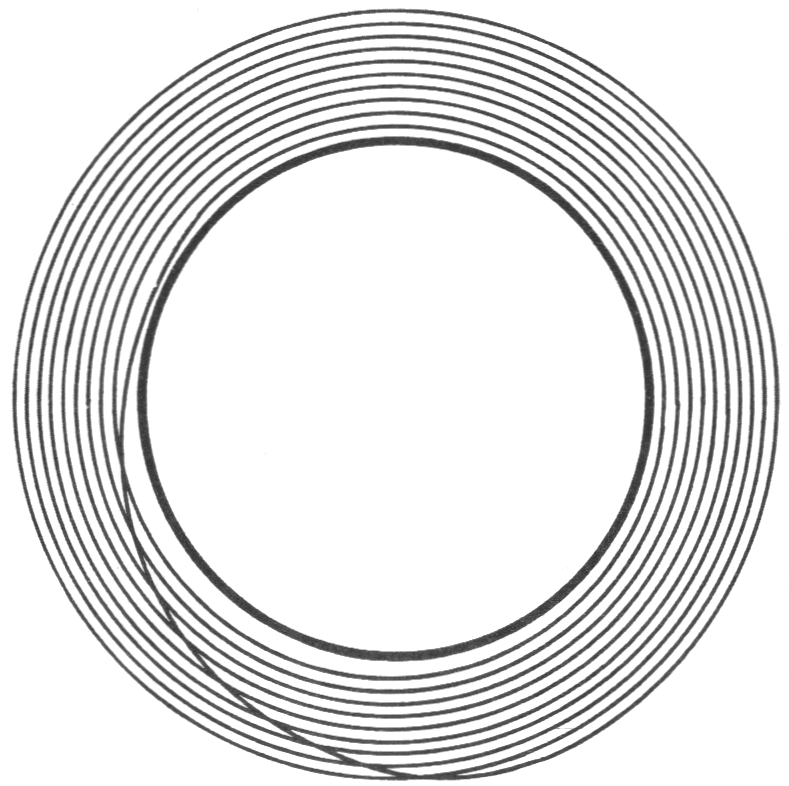
图9 拉伸一个圆使它绕自身10次
假设初始的 x 值为 0.255 437 86,我们来看看每次迭代得到的新 x 值:
迭代次数 x 值
0 次 0.255 437 86
1 次 0.554 378 6
2 次 0.543 786
3 次 0.437 86
4 次 0.378 6
5 次 0.786
6 次 0.86
7 次 0.6
8 次 0.0
从第 8 次迭代开始,以后所有迭代所得的 x 值将都是 0 了。因此,可以说迭代收敛(稳定)了。但我们应该清楚,这种迭代之所以收敛,是因为我们最初给出的 x 值的小数位数有限,该数值是离散的。而自然界真实的数将有无限多的小数位。
对于上述的像螺线管那样 10 圈包绕的迭代运动,有如下奇特的特性:
(1)对初始条件的敏感性
我们需要通过示例说明该性质。再次给出两个不同的 x 初值。第一个值包含 π 的所有小数位的,它具有无限多的小数位,姑且仍称其位 π。第二个值的前 10 亿个小数位与 π 的前十亿个小数位相同,但后面变为 1212121212… 永远持续下去,我们称其为 π’。这两个值是如此相近,他们在以上 10 重包绕的迭代运动中,结果会有差异吗?
答案很容易给出,在前十亿次迭代中,初值 π 和 π’ 的迭代结果相同。但在之后,两者的结果就不同了,π’ 将在 1 和 2 之间振荡,而 π 将继续游历 π 的更多小数位。因此,两个相互极其接近的初始条件,最后却以完全无关的结果而告终。
(2)无规旅程的存在性
只要给定的初始点各小数位的出现是无规律的,点的运动将完全没有规律可循。
(3)无规旅程的共存性
区间 [0, 1] 之间“几乎所有”的小数都有无规的十进制展开式,所以针对几乎所有的初始点,点的运动都具备这种无规律特性。
(4)周期性/非周期性紧密混杂
什么时候迭代结果具有周期性,什么时候没有周期性呢?其实只要给定的初值是有理数,即它是整数 p 和 q 构成的分数 p / q,则迭代结果将具有周期性;否则,迭代结果是非周期性的。由于任何两个无理数之间都有有理数,因此导致周期运动的初始点和不导致初始运动的初始点,就像糕饼中的糖和面粉那样混在一起。这还意味着,周期点都是不稳定的——如果你把他们轻微扰动到邻近的无理数,他们就不再是周期点了。事实上,由于实际的数大多是无理数,因此实际的运动大多不具备周期性。
这种螺线管结构相当于把一个圆周线不断地向自身映射,圆上每个点在映射后都得到一个新的位置,该位置的具体坐标不确定,但总能保证其仍处于圆周上。在这种运动中,系统的每个定态都是不稳定的。
这个例子解释了混沌产生的原因及特征,该例子同时也是第 1 章中“计算器混沌”的进一步解释。
人工构建的吸引子
为了寻找新的吸引子,我们决定对庞加莱截面做点狠的——将它拉伸、折叠、再拉伸、再折叠……,这是一种不同于以往的映射。但为了保证映射后得到的东西仍然能投影的最初的庞加莱截面,我们还精心设计其拉伸和折叠的方式,使经过变换后的形状和原来相似。我们也不再使用线段、拓扑盘那样的庞加莱截面了,而是使用一个实体圆环,这个圆环就像美国式的有孔炸面圈,只不过是生的,以方便我们对其进行变形,我们也可以形象化地描述映射过程。我们的炸面圈是三维的,我们可以使用此炸面圈考察四维空间的运动。
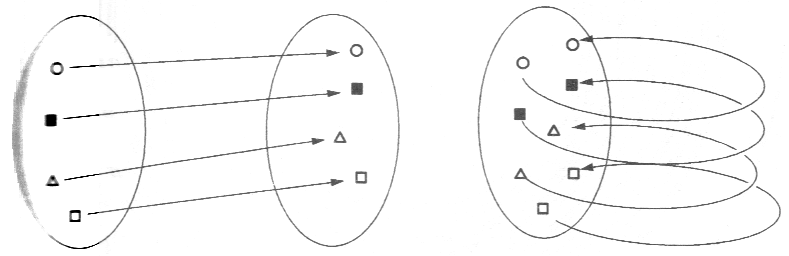
图10 纬垂
下一步的工作,就是考察一个从炸面圈到炸面圈的映射。可是这种映射涉及四维空间的运动,这仍然是我们难以想象的事情。那么,就让我们人为构建一个从炸面圈到炸面圈的映射,我们可以“设计微分方程”——这正是斯梅尔准备做的。这种设计微分方程的过程就是寻找庞加莱截面的纬垂(suspension)。纬垂是庞加莱截面对自身映射的一种几何表示,它是一系列类似圆的曲线,他们被庞加莱截面所截割。曲线从其与庞加莱截面的一个交点处流出,当它下次再次流入截面时,交点的位置正是庞加莱截面向自身映射时所确定的点的位置(图10)。
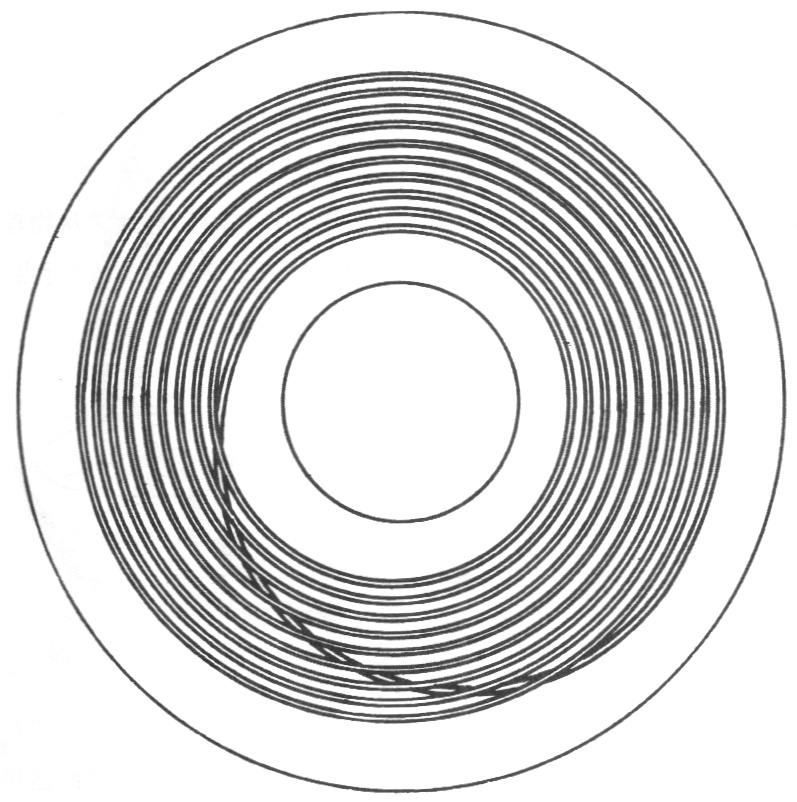
图11 实心环上加以十重包绕
不过斯梅尔完全不用写任何公式,他只需要借助拓扑学原理就可以实现设计微分方程了。如同上面的螺线管运动模型一样,把炸面圈周长扩张 10 倍,使它绕原来的自己包绕 10 圈,且任何点都不多于 1 次(炸面圈上每个点不能同时映射到两个点,那还就相当于将流体撕开了),如图11所示。图中看似有一条线与其他线相交了,其实在三维空间,他们并没有相交。在现实中,我们完全可以用真实的生面做到这种十重包绕。
运动在继续,我们不断地映射,10 重包绕,100 重包绕,1000 重包绕……,如此迭代下去。
工作完成了,来看看我们发现了什么。如果你多次迭代从这环向自身的映射,则所有初始点都愈来愈接近螺线管。所以螺线管是庞加莱截面上动力学的一个吸引子。螺线管的纬垂是整个四维流的吸引子。
想象使这种动力系统稍加更改——将实心环拉伸 10.1 倍而不是 10 倍,螺线管的形态将会稍微改变——它更松弛了,但仍然是 10 圈包绕,我们无法做到 11 圈包绕,即其拓扑性质没发生改变。这就意味着小的扰动不会改变系统运动的拓扑。因而这种运动是结构稳定的,它将有一个吸引子。
螺线管不是单个点,也不是环,所以它不属于传统的典型吸引子。我们称这种不属于经典类型(点或环)的结构稳定的吸引子为奇怪吸引子。
接下来,本章又举了两个例子:康托尔集和康托尔干酪。这是两种分形现象,但作者很克制地一次都不提分形二字。作者只是指出,这些现象也可以用螺线管来描述。
真正的混沌
我们终于找到了另外一种吸引子了——奇怪吸引子,一个可以用螺线管描述的吸引子。该吸引子同螺线管模型一样,有 4 个著名的奇怪特性:对初始条件的敏感性、无规旅程的存在性、无规旅程的共存性、周期性/非周期性紧密混杂。由此产生一个严重的问题,假设有一个具有奇怪吸引子的物理过程,按照经典应用数学的方法,寻找所谓初值问题的解。你会发现,只有当你以无限精度给出初值时,才能得到正确的解。这当然做不到,因此对这种物理过程而言,要想进行长期预测是不可能的。这就意味着,奇怪吸引子必伴随有混沌。
但是,这只是我们人为生造的吸引子,现实世界真的存在混沌现象吗?从理论上来说,只要一种运动在数学中能结构稳定地出现,它在自然界就会可观测地发生。让我们拭目以待吧。