本章将介绍人们首次深入认识的一种自然界的混沌现象——大气运动中存在的混沌,并借此分析混沌的性质。
天气预报
1922年,理查森发表一篇报告《用数值方法进行天气预报》,构想如何用数学方法进行天气预报。其中有一个异想天开的幻想——天气预报厂——基于许多人操控计算器,最终实现实时的、甚至超前的天气预报。
1950年,美国 ENIAC 计算机就作出了天气预报方面首例成功的计算。1953年,普林斯顿 MANIAC 计算机表明,正常天气预报是完全可行的。
用数值方法进行天气预报,实际上是在已知区域内所有点的各种变量初值(气压、气温、适度、风速等),以大气的运动方程作为运动规则,基于对微小时间步长的无限次迭代,得到将来的天气。由于计算模型和计算机精度的原因,我们所构建的看似连续的模拟模型实际上都是离散模型。如在模拟中,时间都是为微小的步长嘀嗒嘀嗒地向前,而不是连续地流逝。所有数只能以计算机所能表达的最小的浮点数的倍数变化。
天气预报的模型非常复杂,用于天气预报的计算机必须以惊人的高速运行。由于模型精细化的欠缺以及在迭代中误差的积累,要在长期时间内精确进行天气预报是不可能的,尤其是无法预报天气模式的突然变化。历史上已经存在很多天气预报的失败案例了。到目前为止,进行长期的天气预报仍然不可能。
洛伦茨吸引子
1963年,洛伦茨发表了著名的论文《确定性非周期流》,在短短 12 页的论文中,洛伦茨预示了非线性动力学的若干主要思想,而这些都是在非线性动力学流行起来之前所做的。本文的摘要可简述如下:可以将流体动力学的解等同于相空间中的轨线,非周期解对小修正而言通常是不稳定的(书中翻译为稳定,属于翻译错误),以致略微不同的初始状态会演变为显著不同的状态;用数值方法进行求解时,发现所有的解都不稳定,几乎所有的解都是非周期解。
洛伦茨的这些结论是通过用计算机模拟空气对流得出的。以下是洛伦茨用于描述空气对流运动的一组常微分方程,该方程是对萨尔茨曼所给出方程的进一步简化,称为洛伦茨方程:
$$\frac{dx}{dt}=\sigma \left( y-x \right)$$ $$\frac{dy}{dt}=x\left( \rho -z \right) -y$$ $$\frac{dz}{dt}=xy-\beta z$$
式中,x, y, z 是三个主要变量,t 是时间。$\sigma$ 称为普兰特尔数,$\rho$ 称为瑞利数。所有的 $\sigma$,$\rho$,$\beta$ > 0,但通常 $\sigma$ = 10,$\beta$ = 8/3,$\rho$ 不定。以下分析多数摘自维基百科洛伦茨系统,可能超出本书目前的知识范围:
- 若 $\rho<1$ 时,所有轨线都指向原点,即系统在原点处存在一个吸引子。由于没有任何其他吸引子,此吸引子也是全局吸引子。在原点处,系统没有对流。
- 若 $\rho=1$ 时,系统发生叉分岔,这种分岔是一个不动点变为三个不动点的一类局部分岔。
- 当 $\rho>1$ 时,出现了两个额外的吸引子,其位置分别是 $\left( \sqrt{\beta \left( \rho -1 \right)},\sqrt{\beta \left( \rho -1 \right)},\rho -1 \right)$ 和 $\left( -\sqrt{\beta \left( \rho -1 \right)},-\sqrt{\beta \left( \rho -1 \right)},\rho -1 \right)$。这两个额外的吸引子都对应于稳定对流。这两个平衡点仅仅在 $\rho <\sigma \frac{\sigma +\beta +3}{\sigma -\beta -1}$ 时才是稳定的。当 $\sigma$ = 10,$\beta$ = 8/3 时,$\rho$ 的临界值是 24.737。
- 若 $\rho =\sigma \frac{\sigma +\beta +3}{\sigma -\beta -1}$ 时,两个额外的吸引子发生分岔,其分岔类型是次临界霍普分岔。当 $\rho$ 大于此临界值后,这两个额外的吸引子消失(即失去稳定性)。
- 当 $\sigma$ = 10,$\beta$ = 8/3, $\rho$ = 28 时,系统表现出混沌特性(但不是所有初值的解都是混沌的)。几乎所有初始点都朝洛伦茨吸引子发展,
维基百科上有使用各种数值计算软件绘制以上系统轨线图的源代码,我们借用其中 Maxima 代码也进行绘制实验。代码如下:
load(dynamics)$
load(draw)$
/* System parameters */
a: 10; b: 8/3; r: 28;
lorenzSystem: [a*(y-x), -x*z+r*x-y, x*y-b*z];
dependentVariables: [x, y, z]$
initialValues: [1, 1, 1]$
timeRange: [t, 0, 50, 0.01]$
/* solution via 4th order Runge-Kutta method */
systemSolution: rk(lorenzSystem, dependentVariables, initialValues, timeRange)$
solutionPoints: map(lambda([x], rest(x)), systemSolution)$
draw3d(point_type=none, points_joined=true, color=blue,
xlabel="x(t)", ylabel="y(t)", zlabel="z(t)",
points(solutionPoints));
以上代码中,位置初值为 (1, 1, 1),改变其中的 r 变量(即 $rho$)的值,可得到如下一系列轨线图。
图1 ρ = 0.5 时的运动轨线 图2 ρ = 1.5 时的运动轨线 图3 ρ = 5 时的运动轨线 图4 ρ = 15 时的运动轨线 图5 ρ = 24 时的运动轨线 图6 ρ = 25 时的运动轨线 图7 ρ = 28 时的运动轨线 图8 ρ = 30 时的运动轨线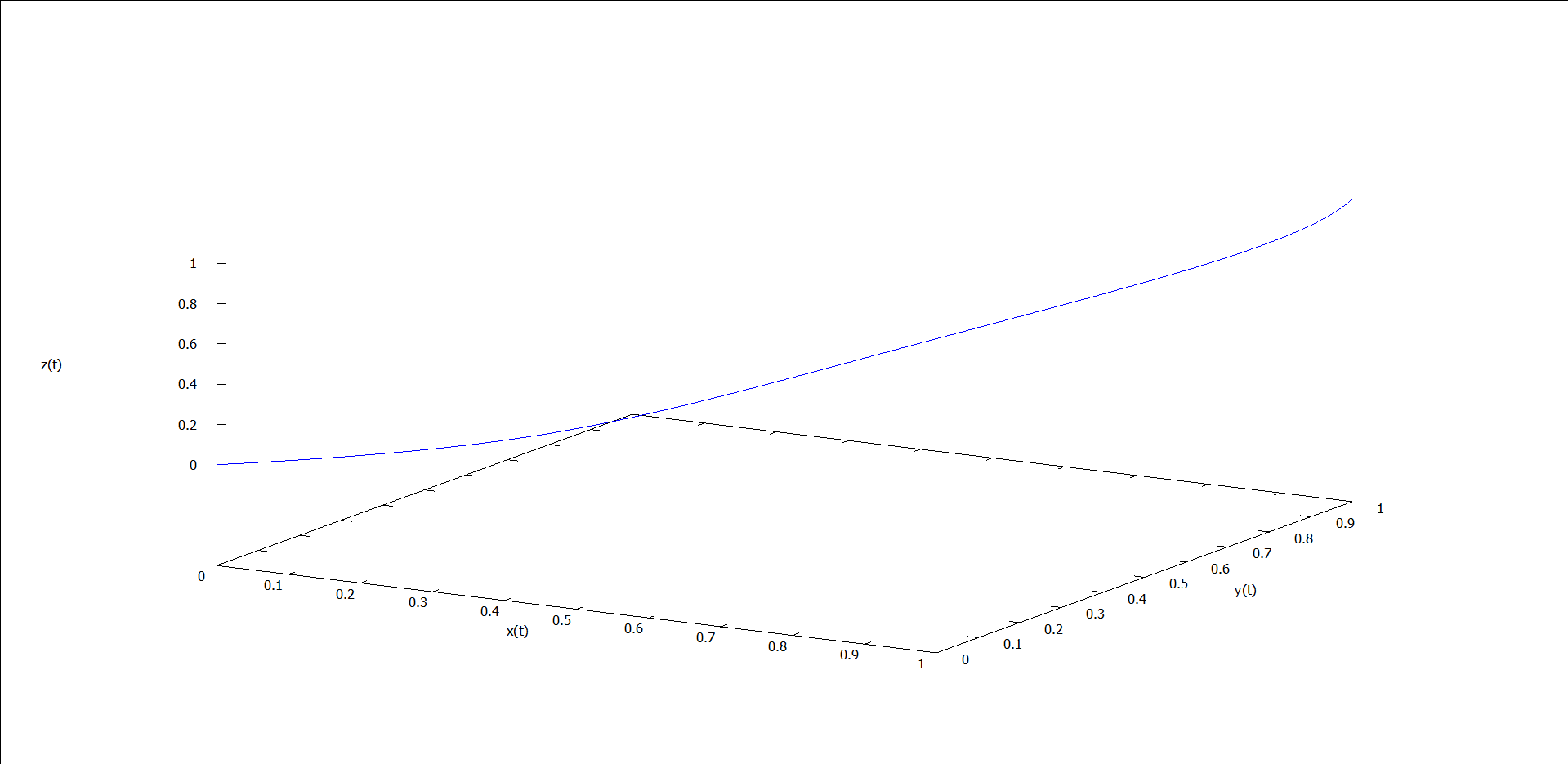
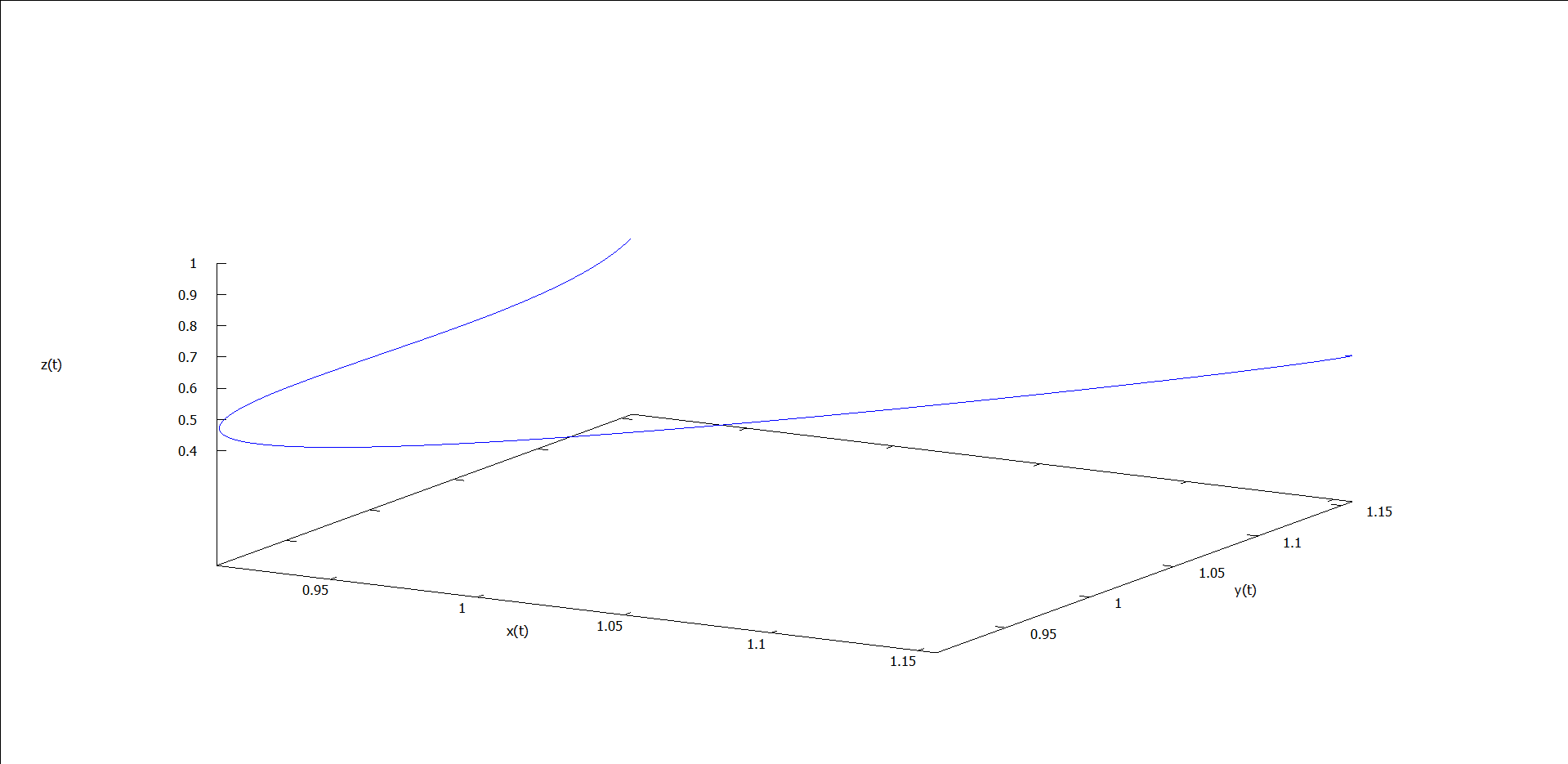
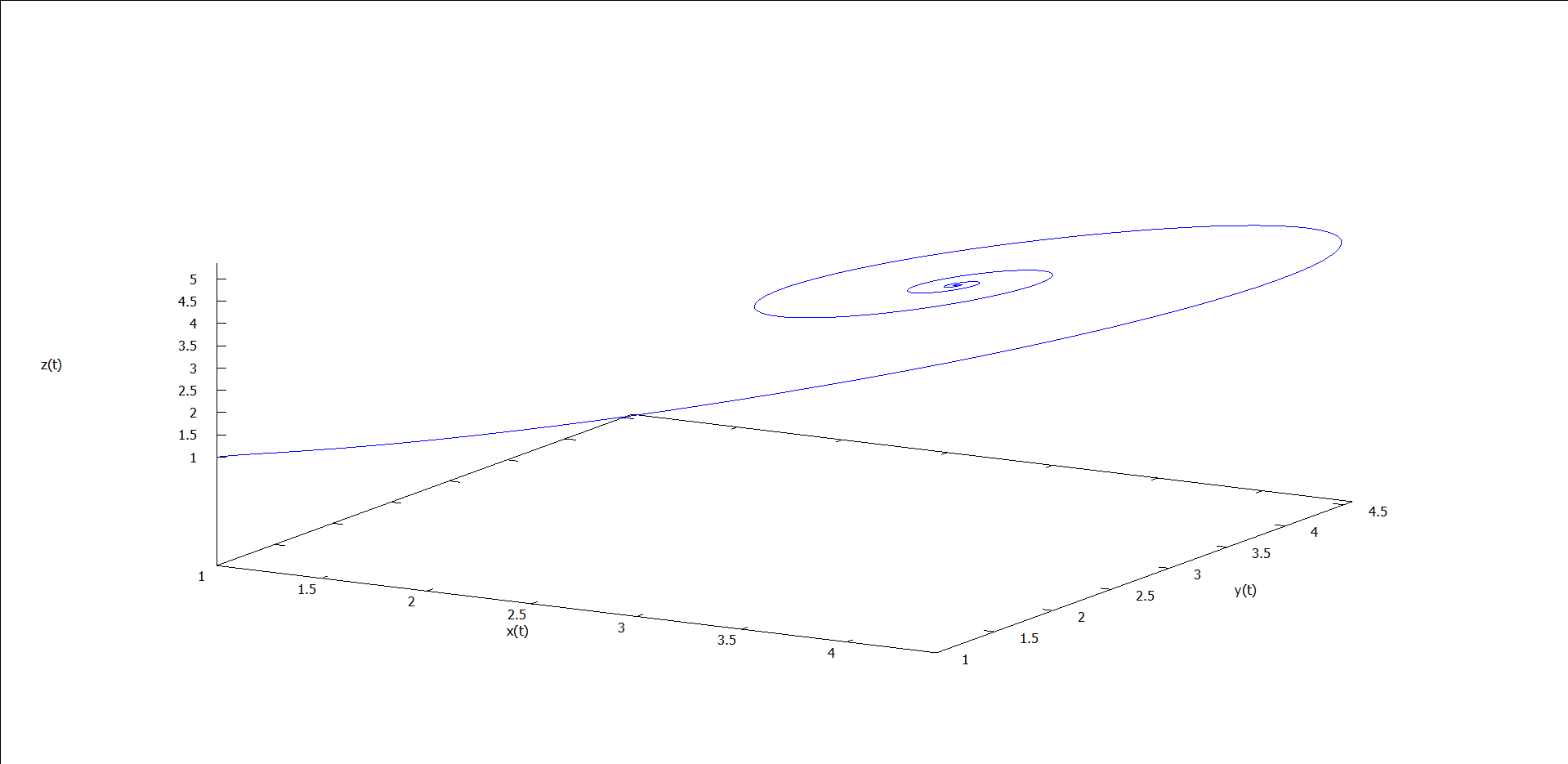
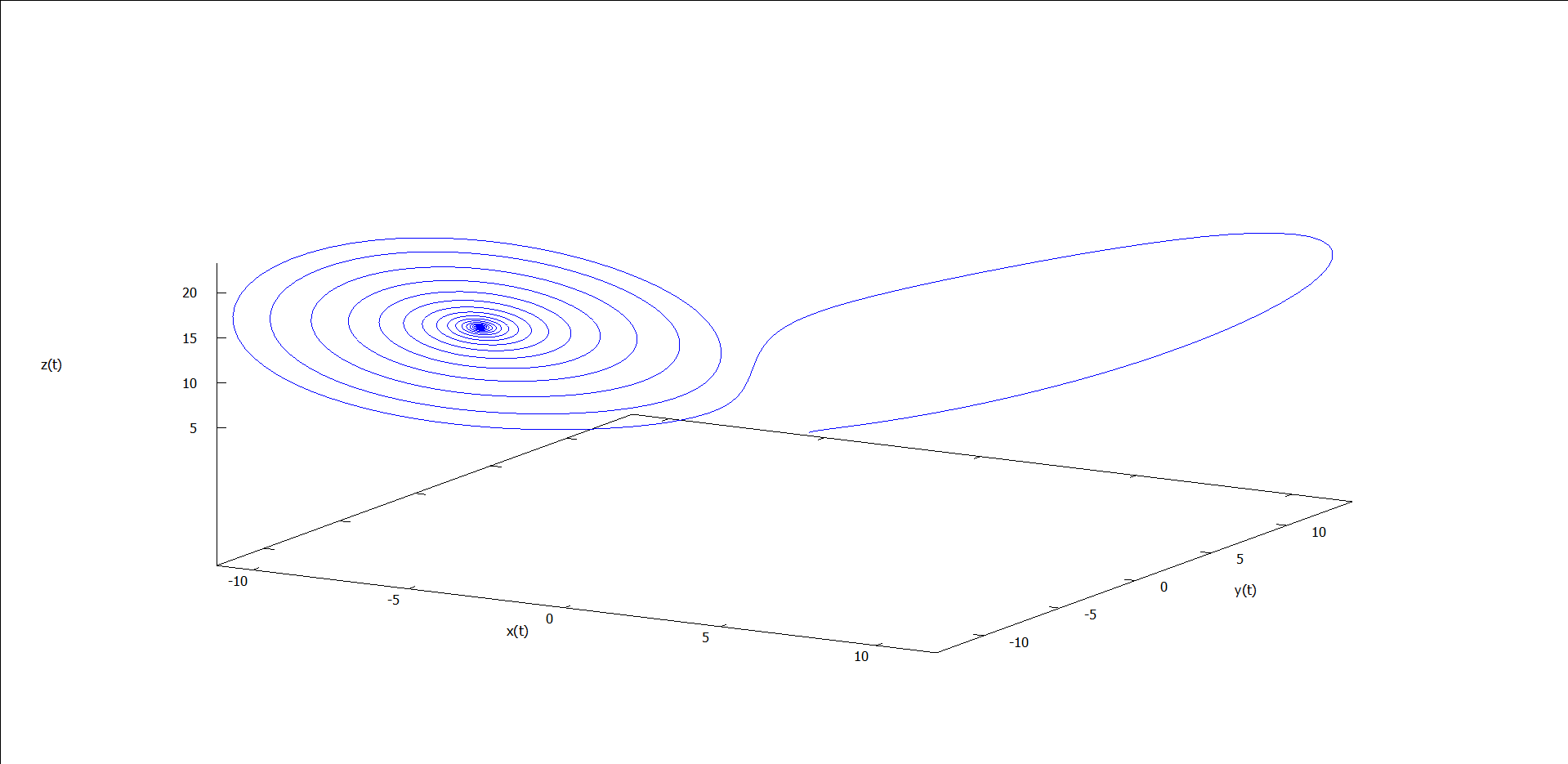
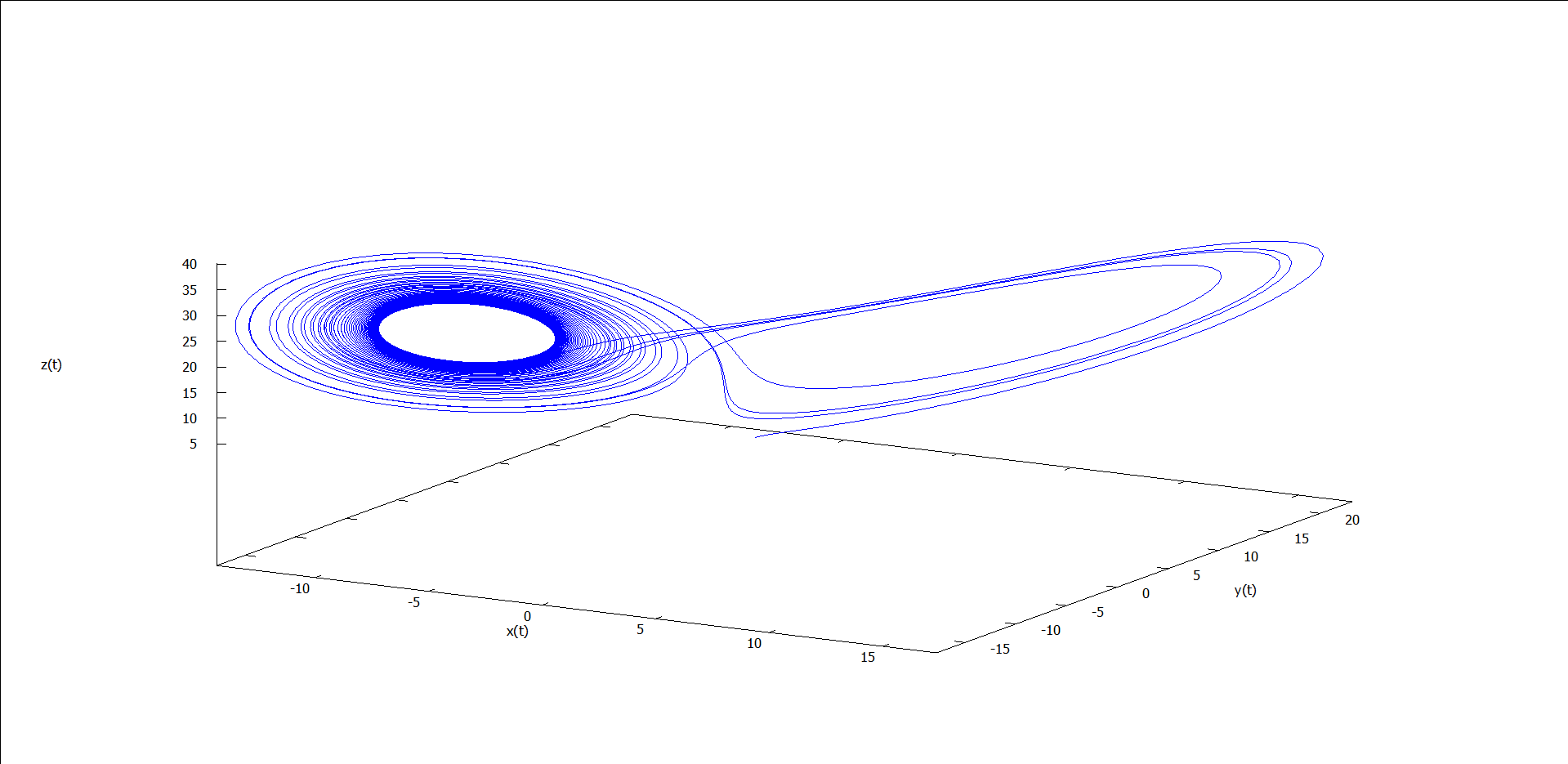
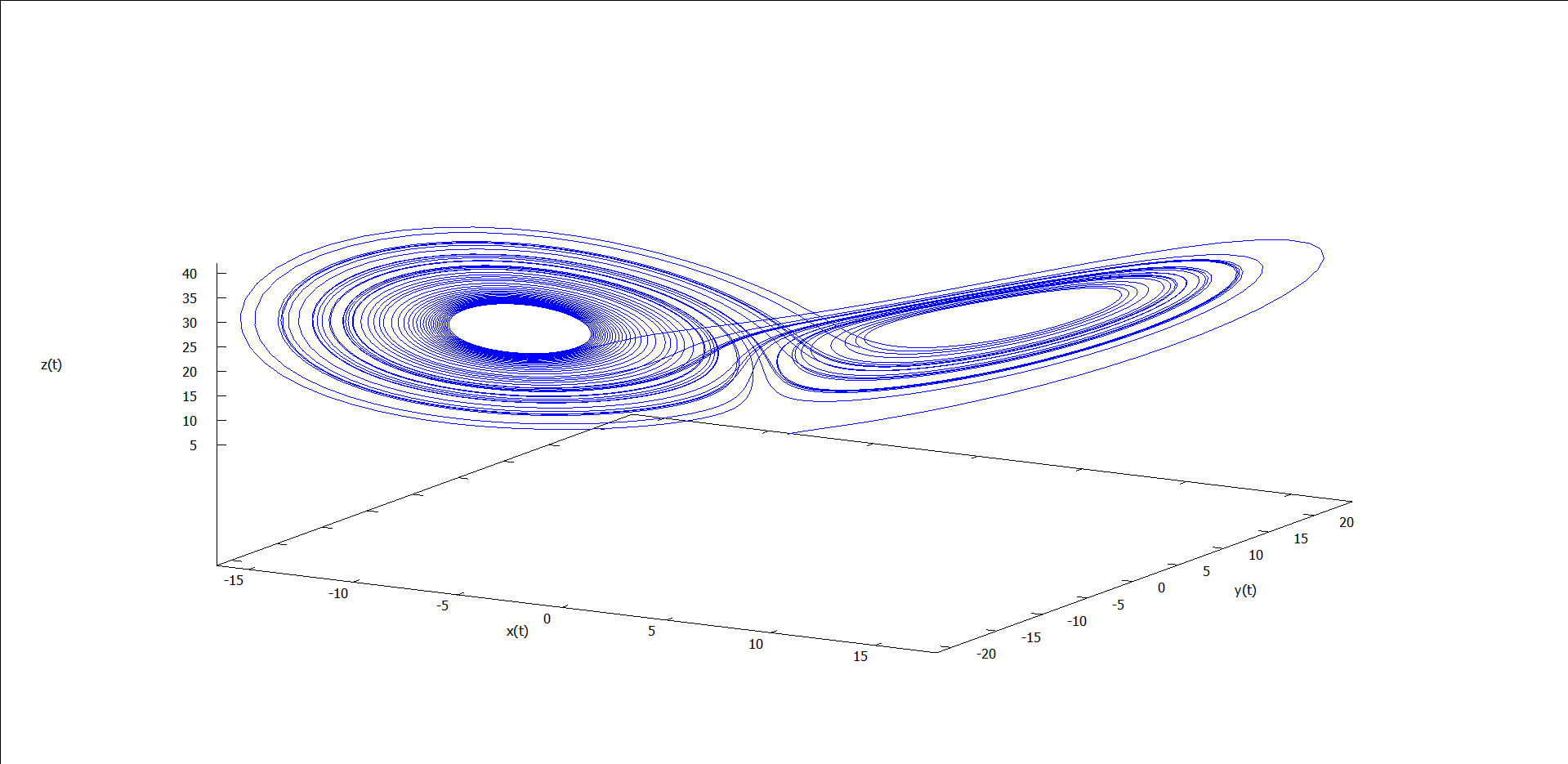
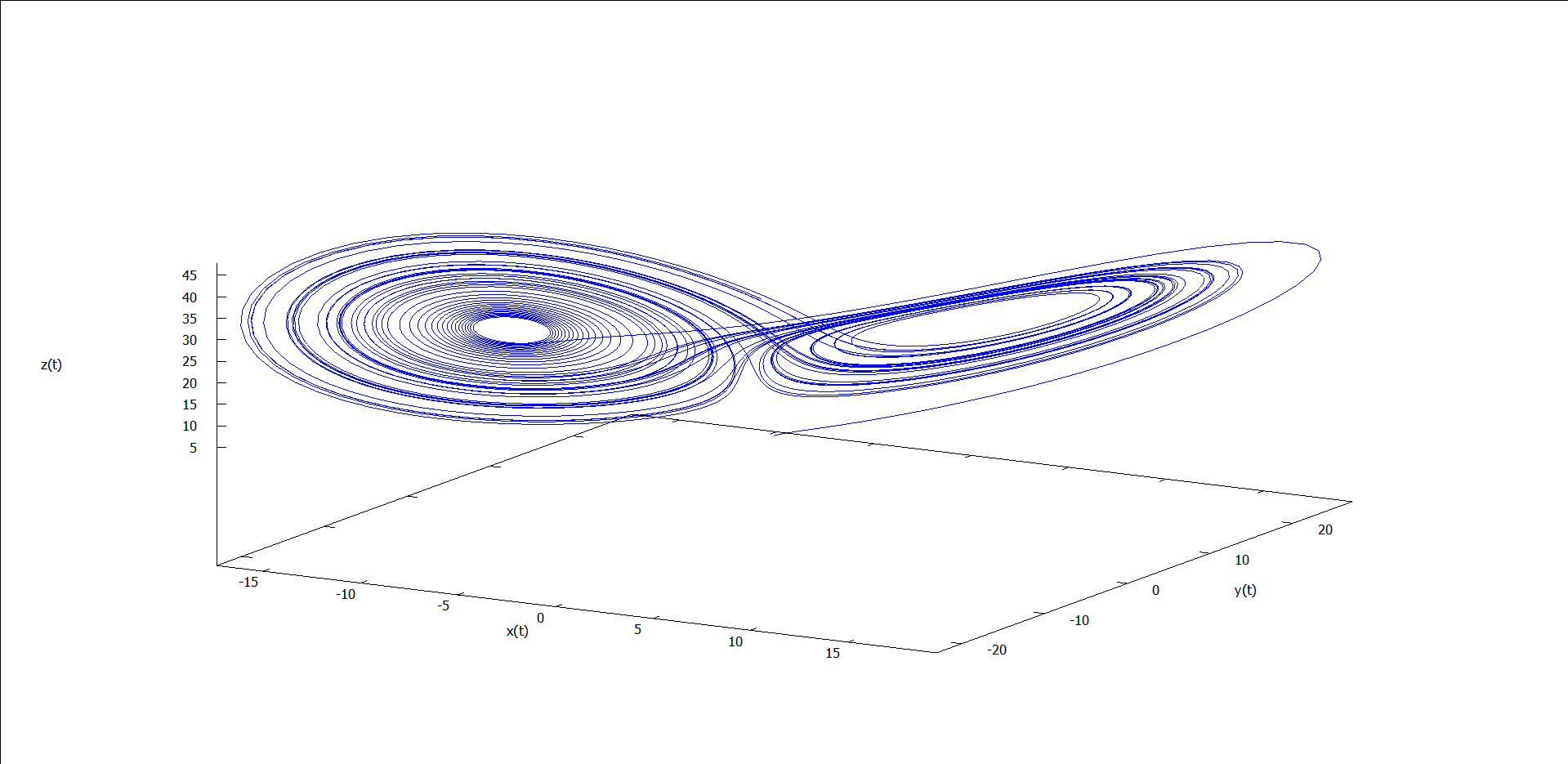
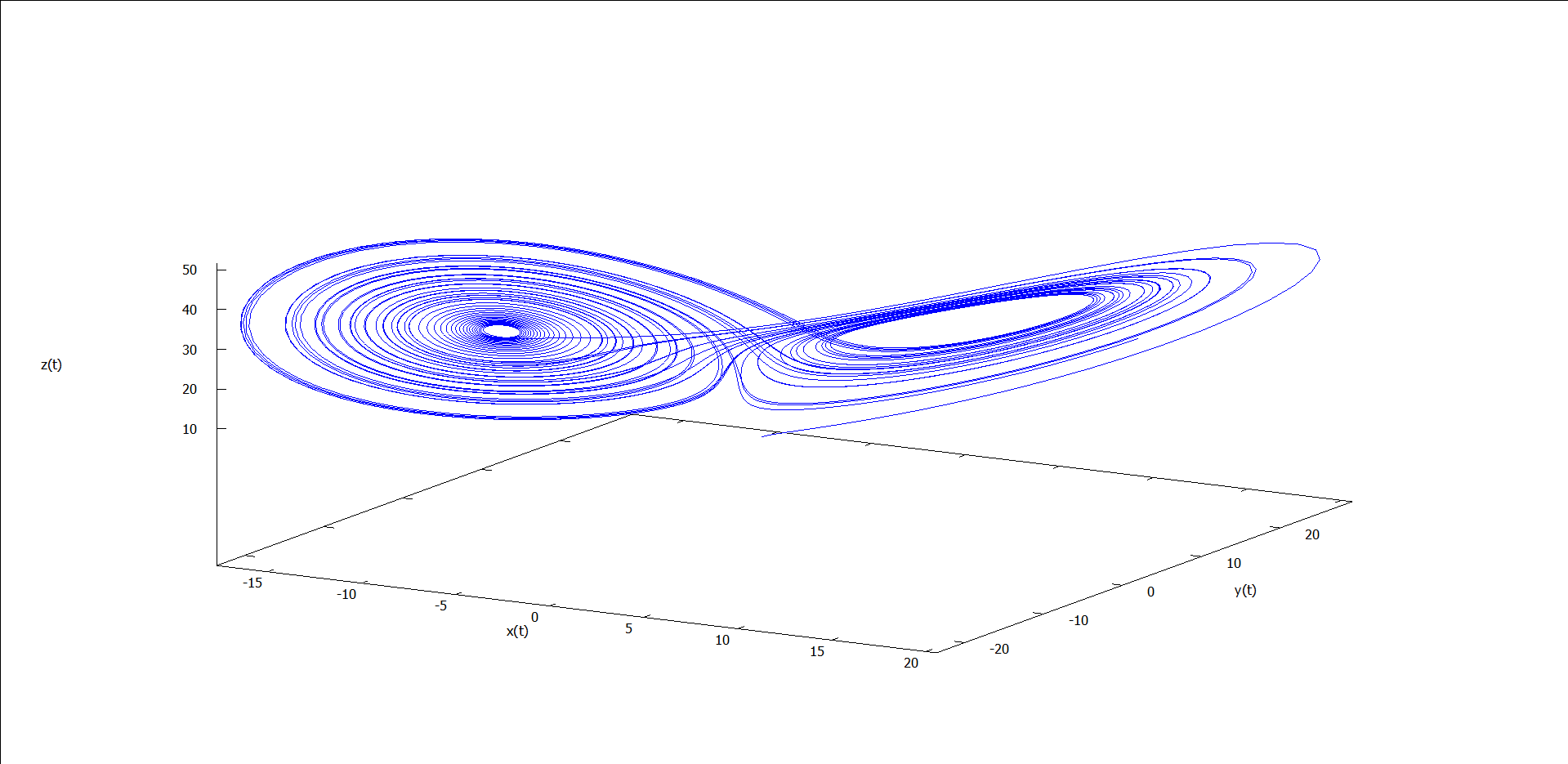
能看出什么吗?似乎能看出点,但又不完全懂——和我一样。我们不关心这么多了,因为这些涉及复杂的微分方程求解的问题,我们只关心图7(ρ = 28)。
图7所针对的 $\sigma$ = 10,$\beta$ = 8/3, $\rho$ = 28 的条件正是洛伦茨论文中所探讨的。为了能进一步看清楚洛伦茨吸引子长什么样子,我们从维基百科得到一个高清版本。如图9所示,其中轨线最初从红色开始运动,并逐渐渐变为蓝色。

图9 洛伦茨吸引子
图10则以动画显示点在洛伦茨吸引子上运动的情况。仔细看这些图,会发现方程的轨线构成奇怪的空间曲面。该图分左右两叶,像肾脏的两叶,又像压扁的椒盐卷饼,越靠图9的上方,两叶分得越开。在图9的上方有两层,下方则合成单层。由于运动轨线不能相交,因此图9的下方看似单层的东西实际上是彼此极其靠近的两层。点经过左右两层的结合部在这些曲面上来回摆动。
图10 洛伦茨吸引子 图11 变量 y 的前 3000次 迭代结果

这样一来,便意味着上面的每一层也是两层(因为下面两层中的每一层运动到上面要变为两层);所以上面有 4 层,所以下面也有 4 层,所以上面将有 8 层,所以……。“存在无限的曲面复形,每一个曲面都相当于接近于两个合并曲面中的一个”——这是洛伦茨的原话。(这段话很难理解,慢慢体会吧)
洛伦茨还给出了前 3000 次迭代中 y 值的变化,如图11所示。可以看出,y 一直在振荡。刚开始,其振幅平稳地增长,但到后来,它发生激烈的振荡,几乎没有任何模式。
蝴蝶效应
似乎没有任何规律性可言,但洛伦茨还是尽力去寻找规律。他取变量 z 的峰值,作出当前峰值与先前峰值的关系。结果是一条极其精确的、中央有一尖峰的曲线。利用这条曲线,只要你知道当前 z 的峰值,就能预言下一刻的峰值——至少还有点规律性。
洛伦茨的曲线实际上是一种穷人的庞加莱截面。他把 z 在每次到达峰值时标绘出来,而不是根据运动的周期以规则的时间间隔标绘出来。虽然存在缺陷,但 z 到达峰值的间隔与运动周期差别不会太大。
图12 变量 z 当前峰值与先前峰值的关系图 图13 蝴蝶效应

洛伦茨还基于这种模拟发现了蝴蝶效应,其发现过程纯属偶然。1961年,他正在研究后来被称作洛伦茨系统的一个前身。他算出了一个解,然后还想研究更长时间间隔内系统的性态。他记下前期运行的一半时到达的数,把它作为新的初始点送进计算机。而前期运行的后一半结果则作为和新开始运行的核对。
本来两次具有相同步数的运行结果应该完全相同的。但事实却不一样,结果分道扬镳了,如图13所示。这很奇怪,但洛伦茨思考后得到了答案:在前期运行到一半时,计算机存储的数是 0.506 127,但打印输出只显示 0.506,他在输入时,也只输入了打印显示的值 0.506。两个数看似差别不大,却最终导致了完全相异的结果。
洛伦茨创造了著名的短语“蝴蝶效应”来专门描述这类现象:初始条件的微小变化,将能带动整个系统长期且巨大的链式反应。洛伦茨分析了难以长期准确地进行天气预报的原因:天气不是周期性的,任何表现出非周期性的物理系统都是不可预言的。不过如果天气的变化存在类似态,或拟周期态,进行长期的预报尚有可能。长期究竟有多长,他尚无法确定,“想象中它可以是几天或几个世纪”。现在看来,“几个世纪”已被排除,“几天”看来是正确的。
短语“蝴蝶效应”所能引发的联想是生动的,但或许有点过头了。因为它更多地强调混沌变化无常、不可预测的本性,容易导致混沌的另外一个本性被忽略——稳定性——这正是吸引子的含义。混沌是稳定性和不可预测性的奇妙组合体。
把混沌设想为彻头彻尾的不可预测是错误的。它取决于你想预测什么。如果你知道混沌系统中一个点现在的位置,想预测它在遥远的未来的位置,你会遇到难题。另一方面,你可以很好地预测系统在受到随机扰动后将要回到的单个或几个吸引子(具体要回到哪一个吸引子,却不容易预测)。
那么,如何根据不同时刻对系统测量所得出的时间序列数据,判断系统是否有吸引子呢?正如庞加莱认识到的,吸引子的动力学特性是回复的。也就是说,系统的状态反复接近吸引子的每一个点,特别是回到任一先前状态。这就如同在田野里吃草的牛,它的详细运动时不可预测的,但长期来看,草地里的每一片草都将会被牛一次次光顾。
混沌的时间序列由回复基序的呈现所刻画。更为强烈的是,时间序列的每一个短的子序列将会不明确地回复。因此,如果有一个呈现某个特定波浪模式的时间序列,但再未出现,它就不会位于吸引子上。(这两句话不太好理解,大概是说如果处在同一个吸引子上的两个点足够近,则在接下来的短时间内,两个点运动的特征是相似的,就好像天气变化会出现类似态那样。)这些告诉我们,对应于混沌吸引子的时间序列具有特征脉络,通过适配这一脉络,你不仅可以讲出对应于混沌吸引子的时间序列与不对应于混沌吸引子的时间序列的差别,还可以靠肉眼辨别出两个时间序列是来自同一个混沌吸引子还是来自不同的混沌吸引子。(这句话大概可以用前面“图12 变量z当前峰值与先前峰值的关系图”所具备的规律性来说明,对应于混沌吸引子的曲线有特定的变化规律,而非混沌吸引子应该只是一条平直的线。对于不同的混沌吸引子,其曲线的性状将会不同。)
蝴蝶真的可以导致飓风吗?蝴蝶所干的事就是扰动。它可以使一个位于吸引子上的点仅仅非常短暂地偏离吸引子,但该点会快速回到同一吸引子上,蝴蝶不会把天气扇到一个新的吸引子上。假如未受扰动,它回到点 A,由于受扰,他回到点 B。这两个点位置很近,他们产生短期内具有相同脉络的时间序列。而飓风就是一个特征天气脉络。对于 A 点对应的时间序列未产生飓风,B 点却产生飓风的情况是很难发生的。蝴蝶很难改变特征脉络,它所能干的,通常只是改变飓风发生的时间。当然,蝴蝶也可能会触发或者阻止形成飓风所需的条件,但大多数时候,它对已经就全球原因建立的飓风何时何地将会发生具有次要影响。这样一来,未受扰的 A 点所对应的飓风和受扰的 B 对应的飓风看起来是同一种天气系统,他们只是具有不同的发生时间(而这种时间的改变有可能很小,也可能很大)。
如果说天气对应于吸引子上的某个特定路径,气候对应于整个吸引子。那么蝴蝶只能改变天气,却无法改变气候。而对于气候,它受特定的全球参量(如温室气体的水平)的影响,是可以预测的。
拉伸和折叠
混沌之所以敏感,因为它是两种矛盾趋势的混合体。拿前面的螺线管来说:
- 拉伸:把距离局部扩张,邻近的点被扯开。
- 折叠:把拉伸后的圆绕自身折叠多次,这是用原来的圆容纳拉伸后的圆的唯一办法。这样,尽管相互靠近的点分开了,有些离得很远的点却移近了。
拉伸使得出发时靠近的点发生不同的演化:最初运动还相似,但随着距离越来越远,就相互看不见了,他们的运动就不必相互模仿了。拉伸和折叠的混合体还造成不规则运动。虽然有些点会靠拢,但并不能预知是哪些点将会靠拢。这便是不可预言性。
洛伦茨系统中也发生了拉伸—折叠过程。图10所示的曲面下面的两半都向后绕并叠加,并且在叠加之前,被拉伸到 2 倍宽度。这种奇怪的、无穷多层的双叶曲面必为奇怪吸引子——洛伦茨吸引子。其微分方程虽然是对实际的过度精简,但仍是带有某种物理学血统的切实的三变量方程。这不是拓扑学家精心制造的东西。我们能发现以洛伦茨方程组为模型的真实物理系统,如水轮、发电机和激光器。
洛伦茨打开了一扇通往新世界的大门。