本章将借助“摆”这一经典力学结构,来说明非线性特征是如何出现在看似线性的、简单的系统中,以及如何用几何学描述非线性问题的特征。
摆运动的微分方程
首先来看看用经典的数学物理方法如何对摆进行分析。为了叙述更加准确,这里没有全部采用本书中对摆的求解,而是大量借用维基百科中关于摆的数学分析一文。
建模
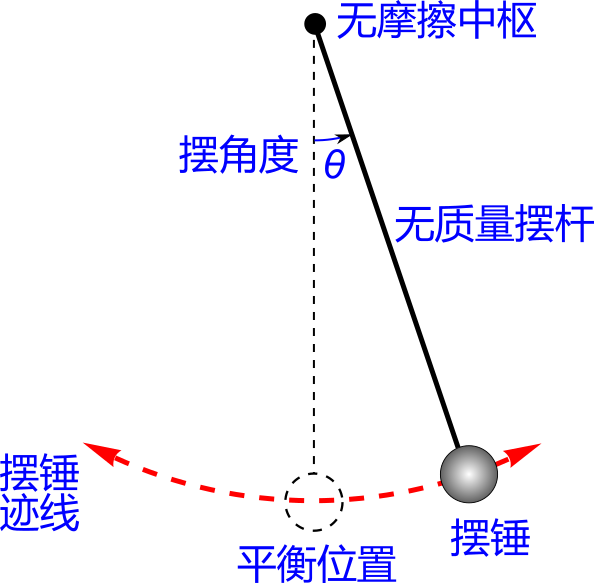
图1 摆
对于常见的摆,我们进行如下假设以简化模型:
- 摆杆是刚性无质量的;
- 重锤的质量集中于一点;
- 运动仅发生于一个平面内;
- 无摩擦阻力和空气阻力;
- 重力场是均匀的;
- 中心点不发生位移。
这样的摆叫做简单重力摆。
描述系统的微分方程
这里统一定义各种变量符号。令 l 为摆长,m 为摆锤质量,θ 为摆锤的角位移(弧度形式),s 为摆运动的弧长,g 为重力加速度,a 为摆锤运动的加速度,t 为时间。如下图所示。
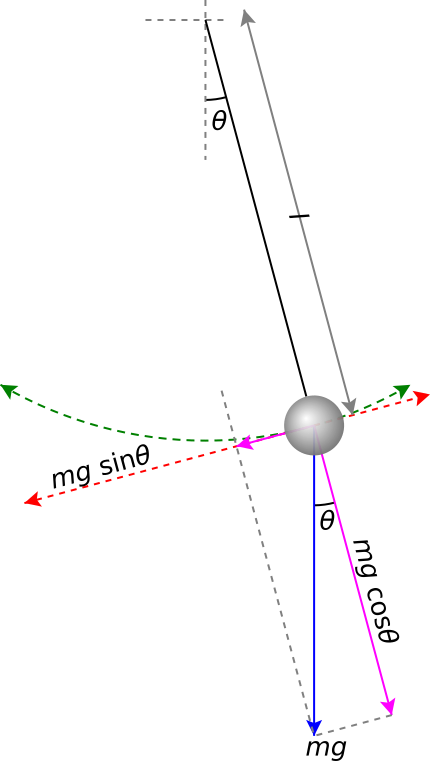
图2 简单重力摆
由牛顿第二运动定律,可知 $$ F = m a $$
重锤所受的不平衡力总是在切线方向(短的紫色箭头),它是重力在切向方向的分力
$$ F=-mg\sin \theta $$
其中的符号表示 θ 和 a 的方向总是相反。根据以上两式,可得 $$ a=-g\sin \theta $$ 重锤运动的加速度可通过以下步骤求得 $$ s=l\theta $$
$$ v=\frac{ds}{dt}=l\frac{d\theta}{dt} $$
$$ a=\frac{d^2s}{dt^2}=l\frac{d^2\theta}{dt^2} $$
$$ l\frac{d^2\theta}{dt^2}=-g\sin \theta $$
最终得式(1)
$$ \frac{d^2\theta}{dt^2}+\frac{g}{l}\sin \theta =0 $$
式(1)就是描述单摆运动的微分方程。该方程也可以通过力矩的定义或能量守恒定律得到。
小角度逼近
式(1)看似简单,但却很难得出用初等函数表述的解。因此,只能进行简化求解,如假设 θ 远远小于 1(通常认为应小于 0.1 弧度),根据小角度近似,有 $$ \sin \theta \approx \theta $$ 式(1)变为谐振子的方程,如下式(式(2))所示 $$ \frac{d^2\theta}{dt^2}+\frac{g}{l}\theta =0 $$ 给定初始条件:$\theta \left( 0 \right) =\theta _0$、$\frac{\mathrm{d}\theta}{\mathrm{d}t}\left( 0 \right) =0$,则式(2)的解为(式(3)) $$ \theta \left( t \right) =\theta _0\cos \left( \sqrt{\frac{g}{l}t} \right) $$ 这种运动式简谐运动,其振幅为 $\theta _0$,其周期为 $$ T_0=2\pi \sqrt{\frac{l}{g}} $$
显然,简单重力摆的运动周期和摆锤的重量无关,而只与摆杆的长度有关,该周期是固定的。
摆运动的拓扑分析
摆运动的相图
现在,我们不满足于进行小角度逼近,而是希望分析任意摆幅时摆的运动特征,甚至可以分析摆围绕旋转中心像螺旋桨那样一圈一圈旋转时的运动特征。很显然,旋转速度可能有快有慢,其运动周期将不再是固定值了。
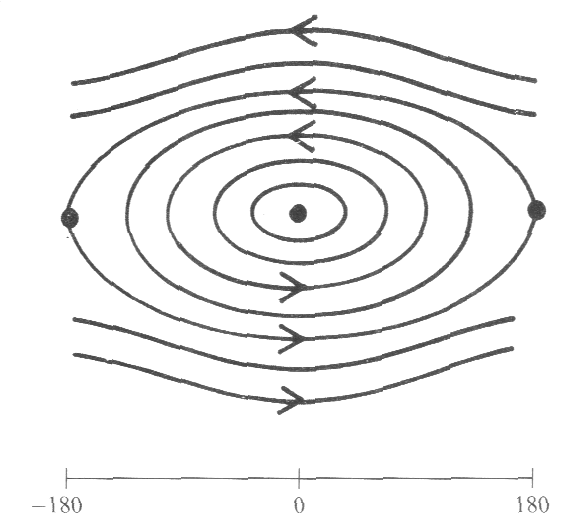
图3 非线性摆的相图
虽然难以求解式(1),我们可以设法以几何的方法分析摆的运动。摆的运动过程中很重要的两个量是摆角 θ 和速度 v。对于特定初始条件的摆,可以设法得出一对对的 (θ, v) 值,将其绘制在以 θ 为横坐标,以 v 为纵坐标的座标系中,将会得到摆运动的轨线。不同的初始条件得到不同的轨线,所有这些轨线绘制在一张图中就是摆运动的相图。
怎么获得 (θ, v) 值对呢?什么方法都可以,比如通过观测得到。不过这里根据能量守恒定律,提供一种计算方法。以旋转中心为零势面,则对于任意角度 θ,摆锤的重力势能是 $mgl\cos \theta$,而其动能是 $\frac{1}{2}mv^2$,根据机械能守恒定律可知 $$ \frac{1}{2}mv^2-mgl\cos \theta =\mathrm{const} $$ 从而可得(式(5)) $$ v=\pm \sqrt{2\frac{\mathrm{const}}{m}+2gl\cos \theta} $$ 根据以上公式,就可以得到 (θ, v) 值对,从而绘制摆运动的相图。如图3所示。
很奇怪的图,就像一个眼睛,上下方都有眉毛,有眼缘(有角的椭圆)。下面针对不同的初始摆幅 $\theta _0$(为了便于理解,这里转而使用角度),分析其运动轨线。
- 当 $\theta _0$ = 0° 时,摆的能量为零,它是静止的,它的运动轨线就是中心点。
- 当 $\theta _0$ < 180° 时,摆的运动轨线是封闭的椭圆,这是摆的标准振荡。这时摆的运动具有周期性(闭合的环代表周期状态)。
- 当 $\theta _0$ = 180° 时,摆的运动轨线对应最外侧的有角椭圆(眼缘线);或者只是眼缘尖端的一点,相当于摆锤静止地处于最高处,显然,这种平衡是不稳定的。
- 当 $\theta _0$ > 180° 时,摆实际绕中心做旋转运动,而其运动轨线对应眼睛上方或下方的眉毛。顺时针对应下眉毛,拟时针对应上眉毛。
摆角为 0° 摆角为 45° 摆角为 90° 摆角为 135° 摆角为 170° 摆角为 180° 摆角为 190° 摆角为 220°


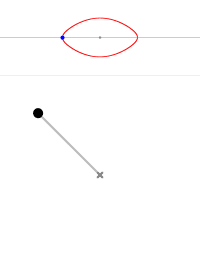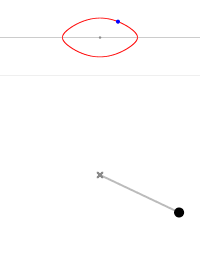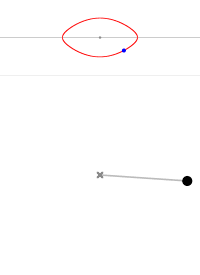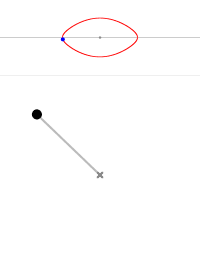
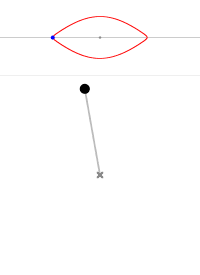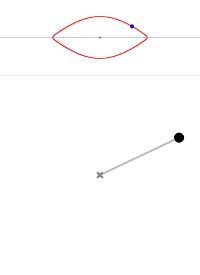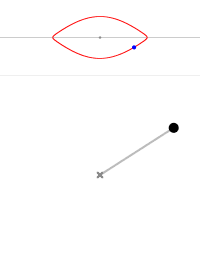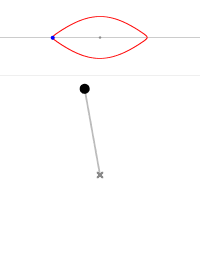
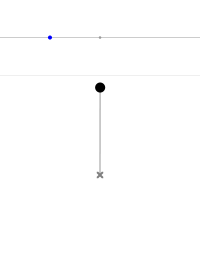
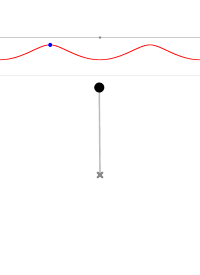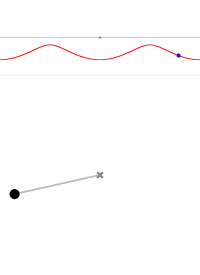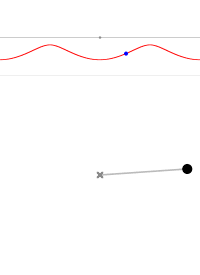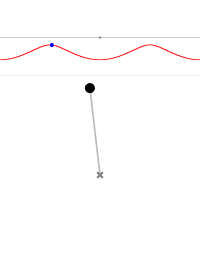
图4 不同初始条件摆的轨线
图3所示的相图给出了摆运动的一幅完整相图,但该图中没有出现时间 t,无法根据该图对每一时刻 t 确定 θ 和 v。这就是我们付出的代价——要想使事情简单,往往必须付出一定的代价。
把它卷起来
图3看起来真的很奇怪,尤其是其眉毛部分。因为我们知道即便摆像螺旋桨那样旋转,它是在做周期运动,可是为什么图中的眉毛却不是一个环呢?摆从 -180° 到 180° 完成一个圆周运动,然而为何左边的 -180° 和 右边的 180° 却相去甚远?
问题不在于摆,而在于我们的坐标系。我们正试图用依靠直线生存的数,来表示依靠圆生存的角度。其解决方法是把图3横向卷起来,让左右两边靠在一起,并使 -180° 和 180° 在实质上重合,如图5所示。这样就可以更加忠实地表示位置(即角度)。至于速度,则不存在类似乎位置这样的不连续问题。
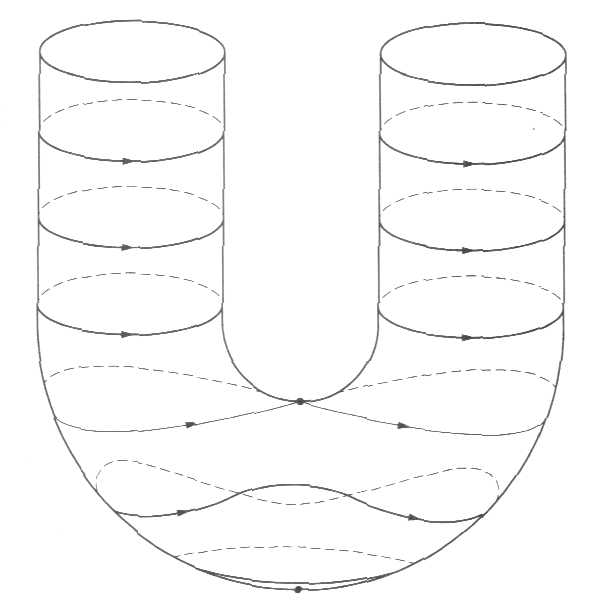
更进一步,我们可以把上面的圆筒弯成 U 形管,这样还可以表示运动的“能级”——越靠上能级越高,如图6所示。从图中还可以看出,在高能级时有两种不同的周期运动(顺时针和逆时针),而在低能级时则只有一种。这些都非常形象真实地反映了摆的运动。
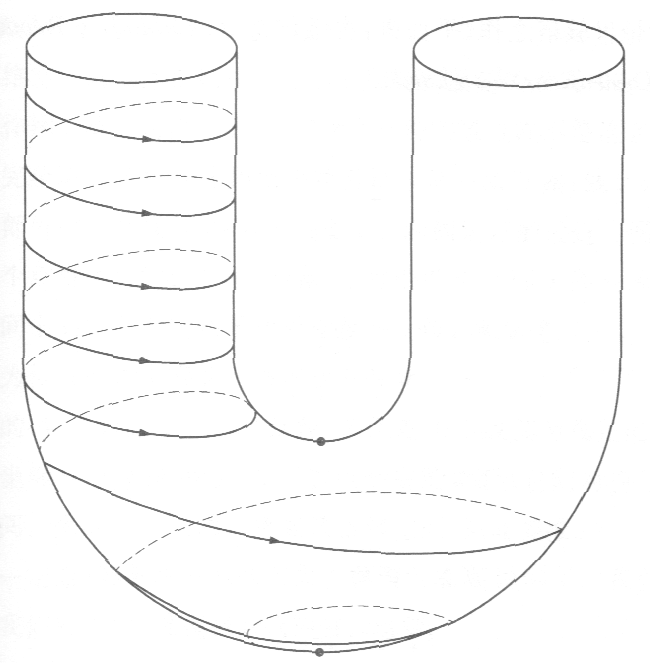
当摆的运动存在很小的摩擦力时,该相图就再次变成如图7所示的情景了。
图5 卷起来的相图 图6 能量守恒的几何示意图 图7 阻尼耗散能量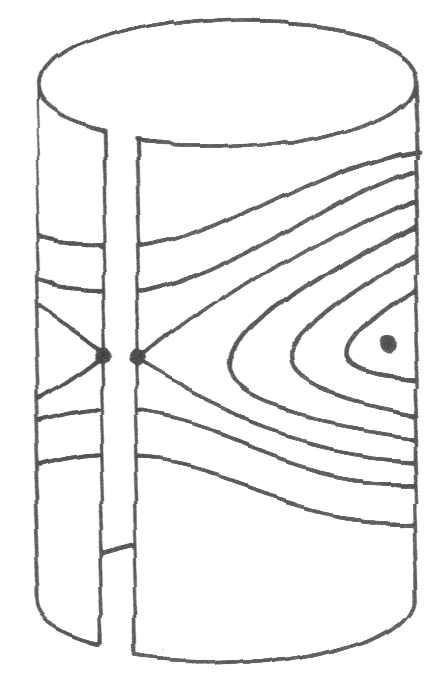
以上说明,我们可以用一幅图来描述摆所有的运动状态。这种图不光可用来研究摆,还可以用来研究非常复杂的动力学系统。几何学和拓扑学是如此有力的工具,使得我们可以用这样的图景取得有关动力学的知识,而这些是经典的推公式的方法完全做不到的,因为根本不存在公式。
线性还是非线性?
现实世界中,我们遇到的许多问题,都像摆一样,既可以对其进行简化的线性分析,又可以进行非线性分析。
由于微分方程具有线性性质,线性分析的最大优点是容易得出其解析解。传统做法是舍弃非线性方程中所有难处理的项,使之线性化。由于方程中略去的项都很小——这是真的,所以线性化方程的解与真实方程的解之间的差异也必然很小——这还有待弄清楚(后文蝴蝶效应表明,这不是真的)。在经典时代,线性化过程已被推向极端,其原因也很实际:我们不能解任何别的方程。线性方程是如此驯良,以致经典数学家愿意损害他们的物理学以换取线性方程。于是经典理论研究的大多是浅波、小变形、低幅振动、小温度梯度等问题。
然而,大自然却无情地是非线性的。如果你随意地画一条线,那不会是一条直线。如果你把手伸进微分方程的摸彩袋,出现非线性方程的概率是无穷大。线性方程的形态也与实际相去甚远,只研究线性方程相当于自我禁锢。甚至可以说,我们从最初用词都是错误的,称一般微分方程为“非线性”方程,就好比把动物学叫做“非象类动物学”一样。正视完整的方程,我们就可以得到一幅更加满意的图景,即使不再能拥有一个可用来获得答案的公式也是值得的。
n 维空间中的动力学
我们已经习惯于生活在三维空间中,或者再加一个时间维成为四维空间,我们的头脑很难想象四维以上的空间。实际上,当我们在考虑一个具有多个自由度的问题时,相当于我们在研究多维空间。如对于三体问题,每一体都有 3 个位置坐标和 3 个速度坐标,所以我们正面对一个含有 18 个不同量的问题,我们正在 18 维空间中思考。
这种对空间维度的重新表述往往一文不值,但在动力学研究中,它却提供了一个优美的几何框架,使得动力学中正在发生的事情更容易被看清。具有 n 个自由度——即 n 个不同变量——的系统可视为生存在 n 维空间里。n 维空间内单个点的 n 个坐标,同时定义了所有 n 个变量。
如果仍然对理解多维空间存在困难,那么就只考虑一个点。以往各种运动定律告诉我们的正是给定的初始点如何在它的空间中沿着曲线(爱因斯坦称它为“世界线”)流动。而不同的初始位置,则对应不同的曲线,这就像流场中的流线一样。
这种将多维系统的运动看作是多维流场中的流线的思想并不是天马行空,而是具有深刻的用意。让我们基于这种思想给出一条定理,以便为下一章的论述做些铺垫:
如果系统是哈密顿系统(即无摩擦),则流体是不可压缩的。
该定理被称为不可压缩性定理,是刘维尔(Joseph Liouville)在19世纪发现的,基于该定律能得出许多惊人的推论。
如果系统不是哈密顿系统(即有摩擦),则仍可将其考虑为流体,但它不再是不可压缩的。对应图7中有摩擦系统中的一滴流体逐渐经过各个能级向底部运动时,其必然收缩(摆的速度和位移乘积变小)。