
图 1 《量纲分析》封面
最近因为要设计“大型煤与瓦斯突出相似材料模拟系统”的缘故,对量纲分析的理论和方法有了初步的接触,尤其是看了谈庆明写的《量纲分析》一书。由此认识到量纲分析是一个在科研工作中非常有用的分析问题的方法,并且其学习和使用也比较容易。这里把我的读书心得写出来,希望能对想要学会这一“招式”的朋友有所帮助。
1 基本概念
量纲:为了辨识某类物理量和区分不同类物理量的方便起见,人们采用“量纲”或“因次”这个术语来表示物理量的基本属性。例如长度、时间、质量显然具有不同的属性,因此他们具有不同的量纲。量纲比单位更抽象,如质量是一个量纲,但千克则是一个度量单位。也可以说,量纲是物理量的种类属性,物理量的量纲反映该物理量的量值随基本量的单位改变而改变的倍数。
有量纲量和无量纲量:物理量总可以按照其属性分为两类。一类物理量的大小与度量时所选用的单位有关,称之为有量纲量,例如长度、时间、质量、速度、加速度、力、动能、功等就是常见的有量纲量;另一类物理量的大小与度量时所选用的单位无关,则称之为无量纲量,例如角度、两个长度之比、两个力之比、两个能量之比等。
量纲的符号表示:物理量的量纲可用一些符号来表示,如用 $L$、$M$、$T$ 分别表示长度、质量、时间的量纲。例如,速度的量纲为“长度/时间”,用符号表示为 $LT^{ -1}$;力的量纲是“质量×加速度”或“质量×(长度/时间)/时间”,用符号表示为 $MLT^{-2}$。在国际单位制中,有 7 个基本量:长度、质量、时间、电流、温度、光强度和物质的量,它们的量纲符号分别为 $L$、$M$、$T$、$I$、$Θ$、$J$ 和 $N$。
量纲的幂次表示:任一物理量$X$的量纲可以表示为一组基本量的量纲的幂次积。例如,对于力学问题来说,任一物理量 $X$ 的量纲(用 $\left[X\right]$ 表示)在长度、质量和时间的$L-M-T$系统中,均可表示为:$\left[ X \right] =L^{α}M^{β}T^{γ}$。
量纲的完整性:反映客观实际规律的关系式必须在单位尺度的主观任意变换下不受破坏。
量纲的齐次性:反映客观实际规律的关系式中所有各项具有完全相同的量纲,也就是每一项的每一基本量纲都有相同的幂次。量纲齐次是构成完整性的充分和必要条件。
说了这么多,现在终于该说什么是量纲分析了。
量纲分析:量纲分析又叫因次分析,英文翻译为 Dimensional Analysis,它是 20 世纪初提出的在物理领域中建立数学模型的一种方法,它在经验和实验的基础上利用物理定律的量纲齐次原则,确定各物理量之间的关系。也就是说,量纲分析就是在保证量纲一致的原则下,分析和探求物理量之间关系。量纲分析的实质是依据量纲的完整性和齐次性,通过对控制现象各参数的量纲分析,来辨识物理现象的类别和认识物理问题的规律。
在介绍量纲分析的方法之前,先介绍一下量纲分析方法的基本原理:$\varPi$ 定理
$\varPi$ 定理:若有一个齐次性的方程,其中若有 $N$ 个变量,而基本量的数目是 $k$,那么一定形成 $N-k$ 个无量纲变量,他们之间形成确定的函数关系。$\varPi$ 定理是根据量纲分析的原理寻求和简化物理量之间函数关系的定理,它说明了所有完整的关系式都可以无量纲化。
$\varPi$ 定理首先是由 Buckingham 在 1914 年提出的。到了 1922 年,P.W.Bridgman 把这个定理成为 $\varPi$ 定理,这是因为 $\varPi$ 这个符号是由 Buckingham 在定理的推导和证明中用来表示无量纲量的缘故。这里对其做更加详细的解释。设由 $N$ 个自变量 $a_1, a_2, \ldots{} a_N$ 描述的物理规律表述为如下函数关系
$$f\left( {{a_1},{a_2}, \ldots {a_N}} \right) = 0$$
在这 $N$ 个变量中,选出 $k$ 个基本量(基本量是指具有独立量纲的那些物理量,它的量纲不能表示为其他物理量的量纲组合),不妨排在前面,他们是 $a_{1}, a_{2}, \ldots{} a_{k}$,而后面的 $N-k$ 个变量是导出量(导出量则是指其量纲可以表示为基本量量纲组合的物理量)。将这 $k$ 个基本量取作单位,上面的函数关系即可化为
$$f\left( 1,1,…1,\varPi _1,\varPi _2,…\varPi _{N-K} \right) =0$$
在以上函数 $f$ 的变量中,最前面有 $k$ 个 1,他们都是不变化的常数,只有后面的 $N-k$个$\varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k}$ 才是对 $f$ 起作用的无量纲变量。因此函数关系可以改写为
$$f \left(\varPi_{1}, \varPi_{1}, \ldots{} \varPi_{N-k}\right)=0$$
需要注意一点,在上述 $\varPi$ 和 $a$ 的表示式中都用 $f$ 作为函数的符号,但两类表示式的具体形式是不同的。用 $\varPi$ 表示的 $f$ 只意味着因变量和自变量之间有着某种函数关系,它并不代表函数的具体形式。
2 量纲分析的方法
在理解了 $\varPi$ 定理之后,再说量纲分析的方法就比较简单了。实际上,量纲分析过程就是应用$\varPi$ 定理对现象各控制参数进行无量纲化的过程,一般可按如下步骤进行:
- 在对某种现象进行初步研究的基础上,找出现象的控制参数 $a_{1}, a_{2}, \ldots{} a_{N}$;
- 写出对现象进行描述的函数关系:$f \left(a_{1}, a_{2}, \ldots{} a_{N} \right)=0$,这里并不需要给出函数的具体形式;
- 分析以上函数关系式中的量纲,找出 $k$ 个基本量和 $N-k$ 个导出量;
- 将导出量的量纲用基本量的量纲表示,得到函数关系 $f \left(1, 1, \ldots{} 1; \varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k} \right) =0$,也可进一步简化为 $f \left(\varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k}\right)=0$;
- 说明在基本量 $a_{1}, a_{2}, \ldots{} a_{k}$ 变化时,为使无量纲量 $\varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k}$ 保持不变,而需要如何改变导出量 $a_{k+1}, a_{k+2}, \ldots{} a_{N}$,从而得出描述现象各控制参数间的基本依赖关系。
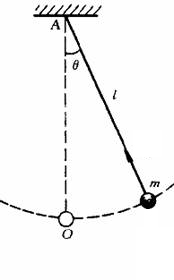
图 2 单摆
在各种参考书中,通常用单摆这样一个简单的例子来对量纲分析的方法和过程进行说明。单摆是由细绳的一端悬挂着的一个具有一定质量 $m$ 的物体,细绳的另一端是固定不动的,而且细绳的质量比悬物的质量 $m$ 小得多而可忽略不计,细绳的变形比绳长 $l$ 小得多也可忽略不计。当悬物从铅垂的自然状态,沿半径为 $l$ 的圆弧挪动到初始方位角 $\theta$,然后放开,物体将在重力的作用下做周期性的震荡。
显然,单被的运动规律由五个控制参数决定,分别是悬物的质量 $m$、细绳的长度 $l$、重力加速度 $g$、初始方位角 $\theta$ 以及单摆的周期 $T_{p}$。于是有以下函数关系
$$f \left(m, l, g, θ, T_{p} \right) =0$$
在该式中,有三个量纲独立的独立量,分别是 $m$, $l$ 和 $g$,他们的量纲分别是质量、长度和加速度。而摆角 $\theta$ 为一无量纲量,周期 $T_{p}$ 的量纲为时间,可以表示为 $l$ 和 $g$ 的量纲的组合。即(长度/加速度)1/2,所以 $\theta$ 和 $T_{p}$ 都是导出量。
我们把 $m$, $l$ 和 $g$ 作为本问题的基本单位系统,用来度量问题中的所有物理量,于是有
$$f \left( 1, 1, θ, T_{p}/(l/g)^{1/2} \right) =0$$
这样得出两个无量纲的 $\varPi$ 数,分别是 $\theta$ 和 $T_{p}/(l/g)^{1/2}$。要是不同的实验条件所反映的规律相同,则必须保证 $\theta$ 和 $T_{p}/(l/g)^{1/2}$ 的取值不变。并且可以通过第二个无量纲 $\varPi$ 数得出影响周期 $T_{p}$ 的因素:
- $T_p$ 与 $l^{1/2}$ 成正比;
- $T_p$ 与 $g^{1/2}$ 成反比;
- $T_p$ 与 $m$ 无关;
- $T_p$ 与 $\theta$ 有关,他们关系的具体形式无法通过量纲分析得出,而需要通过实验或理论分析求得。
这样,我们只需要通过量纲分析,便可得出周期 $T_{p}$ 的各个控制参数,大大简化了需要的实验和分析工作量。
3 模型试验的相似律
量纲分析的一个重要应用是对模型实验相似性的规定和指导。
如果得出了一个现象的无量纲函数关系
$$f \left( \varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k} \right) =0$$
则在进行模型实验中,只要让模型(m)和原型(p)的无量纲自变量 $\varPi_{1}, (\varPi_{1}, \ldots{} \varPi_{N-k}$ 分别对应相等,即
$$(\varPi _1)_m=(\varPi _1)_p,(\varPi _2)_m=(\varPi _2)_p,…(\varPi _{N-k})_m=(\varPi _{N-k})_p$$
即可保证保证模型和原型的无量纲因变量 $\varPi$ 也相等,即
$$\left( \varPi \right) _m=\left( \varPi \right) _p$$
从而保证支配模型和原型的物理法则也相同。
这就是模型实验或数值模拟所遵循的相似规律,简称相似律或模型律,而这些无量纲自变量 $\varPi_{1}, \varPi_{1}, \ldots{} \varPi_{N-k}$,则称之为决定问题本质的相似准数。
用量纲的方法常常很简便,甚至不需要知道具体的定律和机制,便可得到一些重要的概念和信息。然而,正确地运用它并不总是那么容易,难的是主定参量的选择,这要求相当的经验和对现象本质透彻的了解。特别是在那些未知的领域内,更需要有物理上的直觉和洞察力,才能处理得妥切。
4 注意事项
在运用 $\varPi$ 定理进行量纲分析时,需要特别注意以下几点:
- 表示物理规律的函数关系 $f \left( a_{1}, a_{2}, \ldots{} a_{N} \right) =0$ 中的控制参数 $a_{1}, a_{2}, \ldots{} a_{N}$ 必须是自变量,不能混入因变量,也不要加入与问题无关的量,这就要求估计和比较各个自变量对因变量所起的作用,合理决定其取舍。
- 无量纲形式的函数关系 $f \left( \varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k} \right) =0$ 中的函数$f$的具体形式需要依靠实验或理论来求得,一般不能单纯依靠$\varPi$ 定理来得到最后的结论。
- 分析无量纲自变量 $\varPi_{i}$ 的物理意义和量级很有实际价值。如物体上受到三个具有同样量纲的因素的作用,可记为 $F_{1}$, $F_{2}$和$F_{3}$。如取 $F_{1}$ 为单位,从而组成两个无量纲自变量 $F_{2}/F_{1}$ 和 $F_{3}/F_{1}$。若 ${F_3}/{F_1} \ll 1$,则可略去 $F_{3}$ 的作用。
- 如果能够深入知道问题的某些物理本质,或其数学表述,则会对认识因果关系中函数 $f$ 的形式有所帮助。
- 可以肯定,从有量纲形式的因果关系 $f \left( a_{1}, a_{2}, \ldots{} a_{N} \right) =0$ 出发进行实验或分析计算,不如从无量纲形式的因果关系 $f(\varPi_{1}, \varPi_{2}, \ldots{} \varPi_{N-k})=0$ 出发进行实验或分析计算来得简便。这样省去了单位换算的麻烦,减少了自变量的个数,并且使得到的结果更加具有普遍性。
参考文献
- 谈庆明. 量纲分析[M]. 中国科学技术大学出版社, 2007.
- Wikipedia contributors. Dimensional analysis [G/OL]. Wikipedia, The Free Encyclopedia, 22 June 2009 16:13 UT. http://en.wikipedia.org/w/index.php?title=Dimensional_analysis&oldid=297936705